DSSR-PyMOL cartoon-block schematics: PDB entry 175d

PDB-id

175d; SNAP-derived features in text and JSON formats

Class

DNA

Method

NMR

Summary

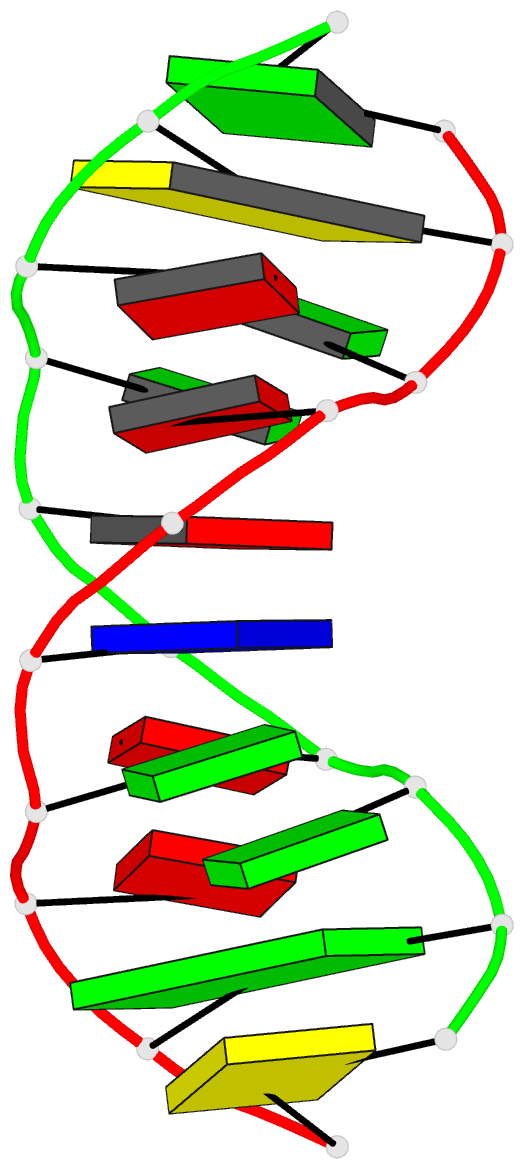
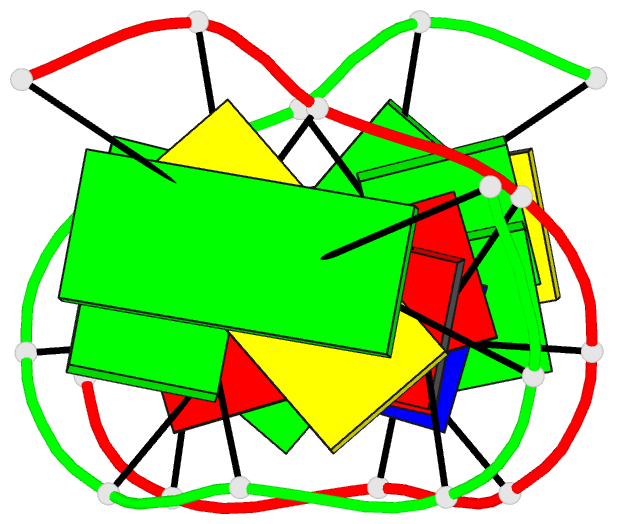
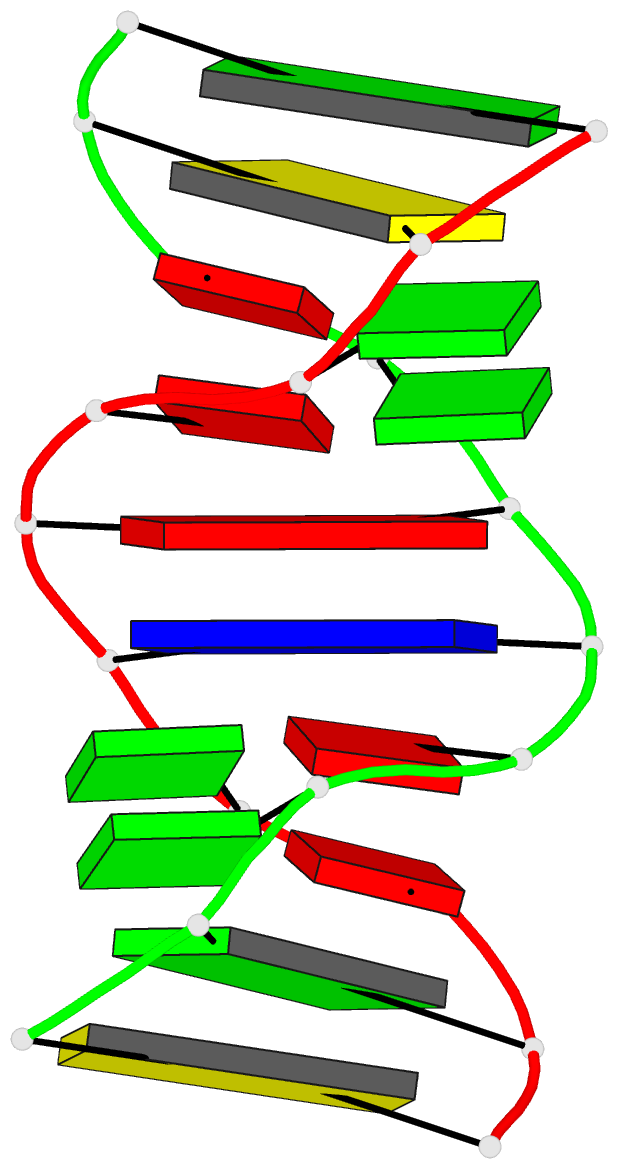
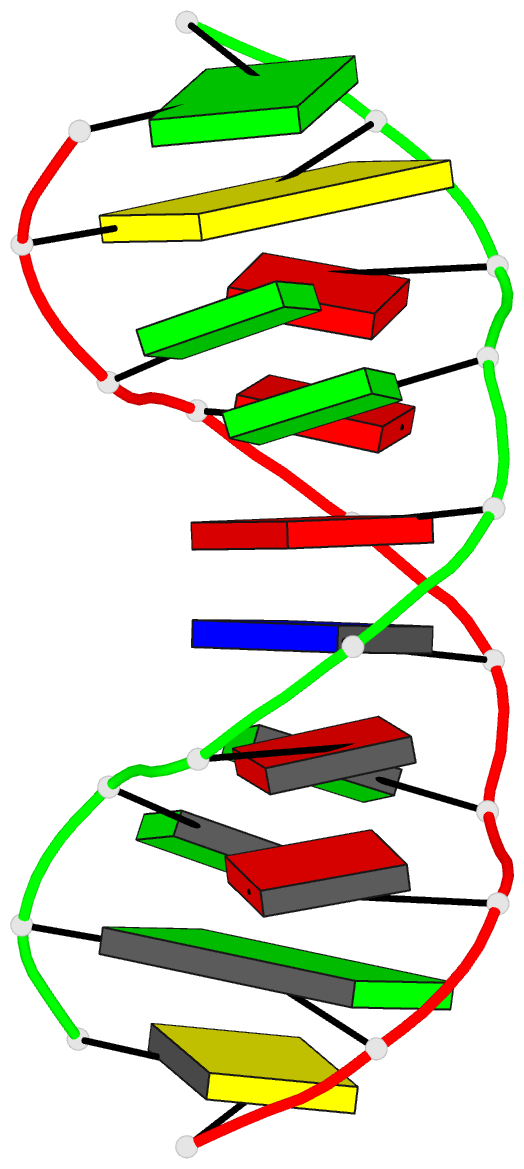
The DNA sequence gcgaatgagc containing the human centromere core sequence gaat forms a self-complementary duplex with sheared g:a pairs in solution

Reference

Chou SH, Cheng JW, Fedoroff O, Reid BR (1994): "DNA sequence GCGAATGAGC containing the human centromere core sequence GAAT forms a self-complementary duplex with sheared G.A pairs in solution." J.Mol.Biol., 241, 467-479. doi: 10.1006/jmbi.1994.1521.

Abstract

The DNA sequence dGCGAATGAGC has a well-resolved, two-dimensional nuclear Overhauser (NOESY) spectrum that is suitable for high quality solution structure determination by NMR methods; in solution this sequence forms a stable self-complementary duplex containing sheared G.A base-pairs. A total of 220 distance constraints derived from time-dependent NOE measurements were collected and refined by repeated back-calculation of the NOESY spectra. Distance information from imino proton studies and from exclusive two-dimensional correlated spectroscopy (E. COSY) and/or linewidth analysis was included in the structure calculation using the program DSPACE 4.2, followed by restrained energy minimization with the program DISCOVER using the AMBER force field. The energies of the distance geometry (DG) structures decreased rapidly in the first few cycles and approached -510 +/- 3 kcal after 1000 cycles of conjugate gradient minimization (about 540 kcal lower than in the initial DG structures). All 15 final DG structures converged to a single family of closely related structures with pair-wise r.m.s.d. values of 0.96 +/- 0.34 A, which was further reduced by energy minimization to 0.70 +/- 0.35 A. Rather unusual structural features of the duplex are revealed in the final structures. The results indicate that, in addition to normal sequences with standard base-pairing, unusual nucleic acid structures can also be determined in solution with quite high precision by NMR/distance geometry methods.